TAREA 3

PARÁMETROS HÍBRIDOS PARA REDES DE DOS PUERTOS

1. Un puerto (o puerta) es un par de terminales donde se verifica que la corriente que ingresa por un terminal es igual a la corriente que sale por el otro. Si un circuito presenta dos pares de terminales se lo denomina red de dos puertos o cuadripolo.

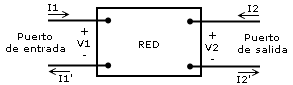
El estudio de los circuitos en las redes de dos puertos que cumplan las siguientes condiciones:

§ que no contengan energía almacenada, es decir con condiciones iniciales nulas;

§ que tampoco contengan fuentes independientes; y

§ donde los puertos no se interconecten externamente

Los cuadripolos son de gran utilidad para simplificar el análisis de circuitos. Cuando no interesan los valores de las variables internas, el circuito puede considerarse como una "caja negra" y por consiguiente ser modelado con apenas dos ecuaciones simultáneas.

REDES DE MULTIPUERTOS

2. Parámetros híbridos
En un sistema de cuatro terminales existen cuatro variables de circuito: la tensión y la corriente de entrada, y la tensión y corriente de salida. Estas cuatro variables se pueden relacionar por medio de algunas ecuaciones, dependiendo de cuales variables se consideren independientes y cuales dependientes.

Así, es posible formar seis sistemas de ecuaciones:

§ (V1,V2) = f (I1,I2) y su inversa (I1,I2) = f (V1,V2)

§ (V1,I1) = f (V2,I2) y su inversa (V2,I2) = f (V1,I1)

§ (V1,I2) = f (V2,I1) y su inversa (V2,I1) = f (V1,I2)

El par de ecuaciones de parámetros híbridos (parámetros h) (y su circuito equivalente) se utiliza a menudo para análisis de circuitos con BJT (transistores bipolares de unión).

Análogamente, se pueden obtener los parámetros:

· y = parámetros admitancia

· z = parámetros impedancia (se dan en Ohms)

· a = parámetros transmisión o parámetros ABCD

· b = parámetros transmisión inversa

· h = parámetros híbridos (empleados en el análisis de circuitos con transistores)

· g = parámetros híbridos inversos

Cuando se utilizan los parámetros híbridos para describir una red de transistores, el par de ecuaciones se escribe como sigue:
Donde los parámetros h se definen como:

h_i = h₁₁ = resistencia de entrada del transistor
h_r = h₁₂ = ganancia de tensión inversa del transistor
h_f = h₂₁ = ganancia directa de corriente del transistor
h₀ = h₂₂ = conductancia de salida del transistor

Si se toman en cuenta éstos parámetros dentro de redes que manejan transistores, ahora tienen que ver con el desempeño del transistor. Cuando los parámetros de entrada y de salida se igualan en forma individual a cero, cada parámetro híbrido representa ya sea una resistencia, una conductancia , una razón de dos tensiones o una razón de dos corrientes.

Es muy útil contar con alguna forma de distinguir entre las tres configuraciones, es decir, EC, CC y BC. Se añade un segundo subíndice a cada parámetro híbrido para proporcionar esta distinción. Por ejemplo, un circuito en EC suele tener h_i en el circuito de base, y se cambia a h_ie. De manera similar para BC, h_i se cambia por h_ib, y para CC, se cambia a h_ic. Los tres valores se relacionan entre sí como sigue

es función del punto de operación (I El valor real de β _CQ) del transistor es. En la porción plana de la curva de i_C contra v_CE con i_B constante, el cambio en β es pequeño. Conforme el transistor se aproxima a la saturación, β empieza a caer. A medida que el transistor se aproxima a corte, β también se aproxima a cero.

Las impedancias se encuentran anulando una de las variables independientes.  Por ejemplo para determinar los valores de los parámetros z, primero se anula I2 (condición de circuito abierto de salida) y se obtiene:

Luego se restaura I2 y se anula I1 (condición de circuito abierto de entrada) y se obtiene:

Para hallar la resistencia de entrada en cortocircuito, es necesario ver el valor de los parámetros antes de abordar la utilización de los circuitos equivalentes para el diseño y análisis. Primero se desarrollan las ecuaciones para h_ie y h_ib, que muestran la dependencia de estos parámetros respecto a la ubicación del punto de operación.

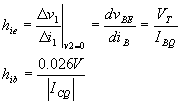
La ecuación anterior es útil para estimar el valor de h_ib.

Parámetros en EC
Las ecuaciones que definen los parámetros de amplificación en ca se derivan en las siguientes secciones. Se proporciona dos ecuaciones de definición para cada parámetro. Estas se denominan como forma larga y forma corta. La ecuación en forma corta es una versión simplificada de la ecuación en forma larga y se deriva haciendo suposiciones acerca de los tamaños relativos de algunos de los parámetros.

Resistencia de entrada, R_en
Se utiliza el circuito de parámetros híbridos para derivar la ecuación de la resistencia de entrada para cada tipo de configuración del amplificador. En circuito equivalente se utiliza para derivar la resistencia de entrada, R_en. En general, b es bastante grande para aproximar 1 + b como b . La corriente en R_E es, por tanto, aproximadamente igual a b i_b.

(1.1)

Si R_B es despreciable comparada con b R_E, la ecuación (1.1) se puede simplificar más hacia la forma.
Ganancia de tensión, A_v
La relación de división de corriente aplicada a la salida de un circuito da

El signo negativo resulta de la dirección opuesta de b i_b con respecto a i_L. Entonces

(1.2)

La ganancia de corriente se encuentra a partir de la formula de ganancia de impedancia, ecuación (1.1).

Resistencia de salida, R₀
La fuente de corriente ideal exhibe una impedancia infinita, ya que se mide la resistencia de salida como la entrada en circuito abierto (es decir, i_b = 0). La resistencia de salida para el transistor EC es entonces

Por lo general, el parámetro h_oe es bastante pequeño como para ser despreciado en los cálculos, de modo que la magnitud de la resistencia de salida del transistor se vuelve infinita.

Se sabe que un transistor opera en forma lineal excepto en las regiones de corte y saturación. La operación en estas regiones o cerca de ellas provoca una reproducción distorsionada de la señal de entrada. Por tanto, se deben evitar estas regiones.

Para encontrar la resistencia de entrada, R_en se considera el circuito ES (emisor-seguidor). Como antes, C₁ y C₂ se consideran cortocircuitos para frecuencias medias.
R_en = R_B

La ganancia de tensión esta dada por
Si h_ib es pequeña comparada con R_E ç ç R_L, como es común, se obtiene la expresión en forma corta
A_v = 1

Ganancia de corriente, A_i se considera como:
A_i = R_B/R_L

La resistencia de salida depende de los parámetros de entrada R_s y R_B, a diferencia del resultado para el amplificador EC, donde R₀ depende solo de R_C.

Parámetros para el amplificador BC
El circuito BC se dibuja a menudo con orientación horizontal.. De esta configuración, es fácil ver que la polarización es idéntica a la del amplificador EC.

La ecuación en forma larga para R_en se deriva en seguida. La corriente en R_en es i_en + (1+b )i_b.

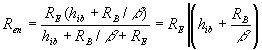(1.3)

La ecuación en forma corta se obtiene suponiendo que h_ib << R_E y R_B << b R_E. Entonces

R_en = h_ib + R_B/b (1.4)

Ganancia de corriente, A_i
La ganancia de corriente para el circuito se encuentra de la siguiente forma:

(1.5)

Entonces, si R_B << b R_E y h_ib << R_E, se obtiene la expresión en forma corta de la ecuación (1.5)

Ganancia de tensión, A_v
La formula de ganancia de impedancia se utiliza para encontrar A_v. Se usan A_i de la ecuación (1.5) y R_en de la ecuación (1.3) para obtener la expresión en forma larga de la ecuación
Si se añade un capacitor de paso entre base y tierra, R_B/b y la expresión se simplifica.

Para la resistencia de salida, R₀, como en el caso del amplificador EC, el generador de corriente dependiente, b i_b, presenta una resistencia elevada por tanto,

R₀ = R_C